Notes

For the ancient Greeks, geography was synonymous with cartography

Examples include Eratosthenes and Ptolemy.

The Greek geographers traced their tradition back to the ancient poets, Homer and Hesiod, followed by Anaximander, "then Democritus and Eudoxus and Dicaearchus, Ephorus and a large number of others; and again, their successors, Eratosthenes, Polybius and Posidonius", as Schiöth abbreviates the list given by Strabo.

Both Homer and Hesiod depicted the earth as a flat circular disc surrounded by the river Oceanus, and Anaximander is credited with the first attempt at a world map on this basis, although lost. It is reconstructed in this example from WM Commons. (FP Note: the dividing lines between continents differ from those accepted later - here the Nile divides Africa from Asia and the Phasis (modern-day Rioni in Georgia) divides Europe from Asia.):

Hecataeus is said to have improved upon Anaximander’s map. Fragments of his Circuit of the Earth have been preserved, which offer some details on his map.

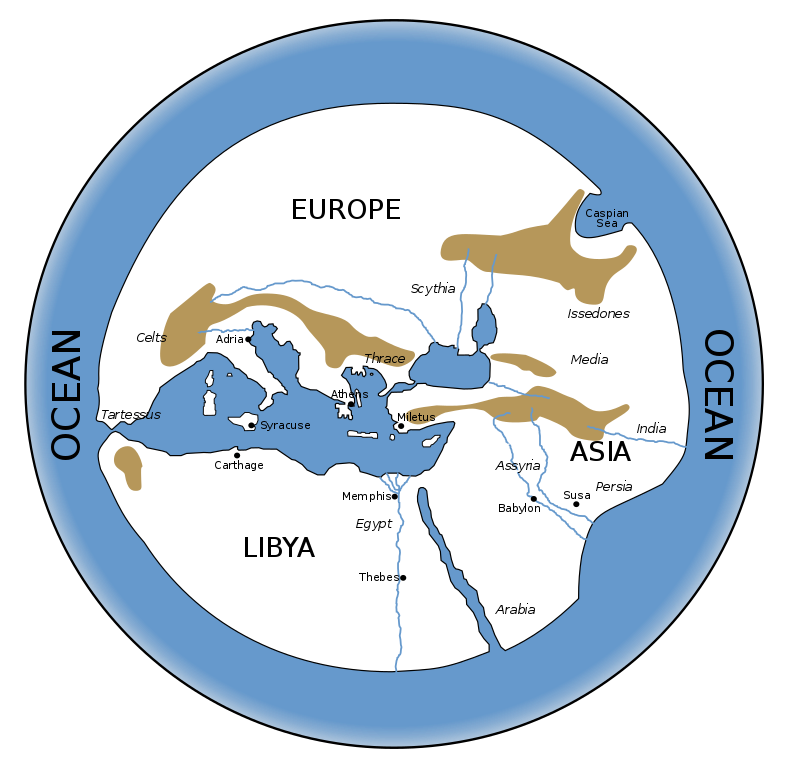
According to Randles (1994), the Homeric model, as represented in the earliest maps of Anaximander and Hecataeus, persisted as one among many other competing models after the discovery of the sphericity of the earth, even throughout the entire Middle Ages and up until the 15th century. It continued to be represented in the medieval Mappae mundi and on the so-called T-O maps, which were the most common type of maps during the Middle Ages (Wright, 1925, pp. 66-68).

There are disputed attributions of the theory of a spherical earth to Thales, the Pythagorean school and Eudoxus. More definitively:

Plato refers to the earth as spherical in the Timaeus (40a; 63a) and Phaedo (97d-99a; 108d-111c) ... This conception of the globe in Plato’s writings 'appears still quite novel and tentative' (Thomson, 1948, p. 114). But the great popularity and influence of Plato’s works helped to establish the tradition of the spherical earth. According to Wright (1925, p. 15), after Plato’s time: ‘no serious thinkers questioned the theory of sphericity.’

Aristotle was certainly the first to provide scientific explanations for the earth’s sphericity (at least in the extant writings), based both on logical deduction and observation, at the end of Book II of On the Heavens (Chapter 14). He provided two sets of arguments, the former based on logical deduction and hypothetical demonstration, the latter based on empirical observation.

logical arguments

‘Its shape must be spherical… to grasp what is meant we must imagine the earth as in the process of generation in the manner which some of the natural philosophers describe… it is the nature of whatever has weight to move towards the centre… it is plain, first, that if particles are moving from all sides alike towards one point, the centre, the resulting mass must be similar on all sides… the extremity must be at a constant distance from the centre. Such a shape is a sphere.’ (Aristotle, On the Heavens 297a; translation in Guthrie, 1929, pp. 247-49).

This argument is curiously akin to a theory of gravitation, assuming that all things 'gravitate' towards the centre, this leads to a uniform distribution of the elements around the centre, leading to the earth being spherical in shape and located at centre of the universe, the points on its surface all laying at an equal distance from the centre. This is despite the fact that Aristotle did not use any such word as 'gravitation', he spoke instead of 'natural motion' towards the centre."

Bertrand Russell provides a good summary of Aristotle’s theory of 'gravitation' and the four elements. This explanation helps to understand the passage in question and place it in its proper context within Aristotle’s philosophy: 'The treatise On the Heavens sets forth a pleasant and simple theory. Things below the moon are subject to generation and decay; from the moon upwards, everything is ungenerated and indestructible. The earth, which is spherical, is at the centre of the universe. In the sublunary sphere, everything is composed of the four elements, earth, water, air, and fire; but there is a fifth element, of which the heavenly bodies are composed. The natural movement of the terrestrial elements is rectilinear [“it is the nature of whatever has weight to move towards the centre” (297a)], but that of the fifth element is circular [the heavenly bodies revolve in a circular motion around the earth]. The heavens are perfectly spherical, and the upper regions are more divine than the lower. The stars and planets are not composed of fire, but of the fifth element; their motion is due to that of spheres to which they are attached. The four terrestrial elements are not eternal, but are generated out of each other - fire is absolutely light, in the sense that its natural motion is upward; earth is absolutely heavy. Air is relatively light, and water is relatively heavy.' (Russell, 1946, p. 198).

empirical arguments

Further proof is obtained from the evidence of the senses. (i) If the earth were not spherical, eclipses of the moon would not exhibit segments of the shape which they do… thus if eclipses are due to the interposition of the earth, the shape must be caused by its circumference, and the earth must be spherical. (ii) Observation of the stars also shows not only that the earth is spherical but that it is of no great size, since a small change of position on our part southward or northward visibly alters the circle of the horizon, so that the stars above our heads change their position considerably, and we do not see the same stars as we move to the North or South. Certain stars are seen in Egypt and the neighbourhood of Cyprus, which are invisible in more northerly lands, and stars which are continuously visible in the northern countries are observed to set in the others. This proves both that the earth is spherical and that its periphery is not large, for otherwise such a small change of position could not have had such an immediate effect. (Aristotle, On the Heavens 297b298a; translation in Guthrie, 1929, p. 253).

Sources

• Schiöth, Tjörvi, (2022). The origins of antipodal theory in ancient Greek science and philosophy. MA Thesis (Univ. Iceland, 2022)

Sources cited by Schiöth (FP note: I haven't checked the quotations in these myself)

• Russell, Bertrand. (1946), History of Western Philosophy
• Wright, John Kirtland (1925), The Geographical Lore of the Time of the Crusades: A Study in the History of Medieval Science and Tradition in Western Europe

Acknowledgements

• Merci pour les cartes, Bibi Saint-Pol